
Regla de L'Hôpital
Uno de los casos de indeterminación que se presenta a la hora de calcular límites aparece cuando queremos resolver un límite de la forma
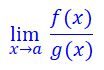
y tanto f(a) como g(a) valen 0. f(a)=g(a)=0. Tenemos entonces una indeterminación del tipo 0/0 que, en ciertas condiciones, se puede resolver aplicando la Regla de L'Hôpital, que dice lo siguiente:
Si f(x) y g(x) son dos funciones derivables en un entorno E de un punto "a" en el que f(a)=g(a)=0 y si además sus derivadas f'(x) y g'(x) son distintas de 0 en todos los puntos del entorno E distintos de "a", entonces
si existe el límite
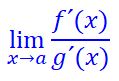
entonces también existe el límite
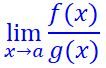
y son iguales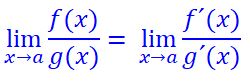
La Regla de L´Hôpital puede aplicarse también al cálculo de límites que presentan las indeterminaciones 0/0 cuando x tiende a ∞ y también se pueden transformar las indeterminaciones del tipo 0·∞, ∞-∞ y algunos otros que puedes consultar en la lista de videos de la Regla de L´Hôpital en Tágoras.
